Bibliografia 

La información que fue encontrada a lo largo del blog fue consultada de los siguientes libros:

1. Geometria, trigonométrica- Lic. L. Galdos.
editorial,cultural.

2.Ecuaciones diferenciales: teoría, técnicas y practicas- George F. Simmons.
editorial, mc graw hill.

3. Álgebra y geometría.
editorial, barnett.

4. Avanza matemáticas 10.
editorial, norma.

Funcion cosecante

Función cosecante 


Se define la función cosecante como el cociente entre la hipotenusa y el cateto opuesto. La cosecante se abrevia, csc.

Dado que csc(x)=1/sen(x), su dominio depende de los valores los cuales la función seno sea igual a cero.
Del estudio de la función seno, obtenemos que la ecuación sen(x)=o se supone para valores de x que x=∩π.

Función de secante

Función de secante 

Se define la función secante como el cociente entre la hipotenusa y el cateto adyacente. la secante se abrevia, sec.

A partir de las lineas trigonométricas descritas para la función y=sec(x) se obtiene la gráfica que se muestra a continuación:

función cotangente

Función cotangente 

La función cotangente se define como el cociente entre el cateto adyacente y el cateto opuesto. Este se abrevia cot.
La función cotangente cot(x)=cos(x)/sen(x) no esta definida para los valores en los que
sen(x)=0, es decir, para los valores de la forma x.

Si utilizamos una calculadora, podemos ver que al tomar valores de x cercanos a los puntos de la forma ∩π, el valor de cot(x) es cada vez mayor (positivo o negativo). Por lo anterior, al gratificar la función cotangente en los puntos de la forma ∩π, trazamos una linea punteada que indica una asìntota vertical.

Función tangente.

Función tangente 

Se define función tangente como el cociente entre el cateto opuesto y el cateto adyacente. La tangente se abrevia, tan.

Llamamos función tangente al resultado de dividir el lado opuesto con el adyacente la hipotenusa.

A partir de las lineas trigonométricas descritas para la función y=tan(x) se obtiene una gráfica para los valores entre 0 y 2 π.

Si construimos una tabla y evaluamos la función para valores entre 0 y π/2 con la calculadora.

Función de coseno.

Función de coseno 

Se define función de coseno como el cociente entre el cateto adyacente y la hipotenusa. Esta se abrevia cos.

Para gratificar la función y=cos(x), recordemos que cos(x+2π)=cos(x), por tanto la función de coseno es periódica de periodo 2π. Con base en la tabla 9.2, evaluamos coseno en valores de x entre [0,2π]. La calculadora debe estar en modo radianes.

A partir de las lineas trigonométricas descritas para la función y=cos(x) se obtiene la gráfica que se muestra para los valores de x.

Características

1. El dominio de la función es el conjunto de los números R.

2. El rango de la funcion y=cos(x) es el conjunto {y∈R/(-14X)<1}

3.La funcion y=cos(x) es periodica y su periodo es de 2π. Esto significa que cos(x)=(x+2∩π) con
∩∈z.

4.La funcion y=cos(x) es par puesto que cos(x) es igual a cos(-x) es decir la funcion y es simetrica respecto al eje Y.

5. La funcion y=cos(x) varia.

Función de seno.

Función de seno 

Se define la función de seno como el cociente entre el cateto opuesto y la hipotenusa. Esta función trigonométrica se abrevia, sen.  

Características

1. Dominio de función seno es R.

2. Es simétrica con respecto al origen O. Es decir, si P(x,y) esta en la gráfica, entonces, Q (-x, -y) también esta en la gráfica. Dado que P(x, sen(x)) esta en la gráfica de la función seno, entonces, Q(-x, -sen(x)) esta en la gráfica de la función seno y, necesariamente, sen(-x)=-sen(x). Por tanto, la función seno es impar. 

3. El comportamiento por cuadrante de la función seno es: 

La identidad sen(θ)= sen(θ+2π ) nos dice que la función seno es periódica y sabemos que su periodo es 2π. Para dibujarla, evaluamos en valores de x entre [0,2π]. Debe recordarse que la calculadora debe estar en modo de radianes.

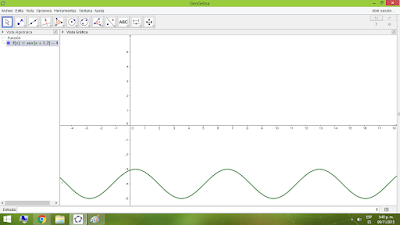
Gráficas que representan la función y=sen(x)

FUNCIONES TRIGONOMÉTRICAS 

Historia 

Rene Descartes Nacido en 1596 y fallecido en 1650 aprovecho el desarrollo del álgebra para combinar los fundamentos de la geometría analítica, que que fue concebida como la síntesis del análisis geométrico con el álgebra. En su honor, las coordenadas empleadas por el para resolver los problemas geométricos reciben el nombre de coordenadas cartesianas.

Definición 

Es aquella que se define por la aplicación de una razón trigonométrica a los distintos valores de la variable independiente, que ha de estar expresada en radianes. Existen seis clases de funciones trigonométricas: seno y su inversa, la cosecante; coseno y su inversa, la secante; y tangente y su inversa, la cotangente. Para cada una de ellas pueden también definirse funciones circulares inversas: arco seno, arco coseno, etc. 

Para construir la gráfica de funciones matemáticas con funciones trigonométricas debemos tener en cuenta los siguientes pasos:

1. Construir la tabla de valores en términos de radianes.

2.Evaluar dicha tabla en la función pero en términos de grados. 

3. Ubicar en el plano cartesiano.

4. Trazar gráfica de acuerdo a los puntos.